Onsite Events

05.01
8:30-18:00
Event Details:
Title:Geometry and Physics Workshop(May 2021)
Date: MAY 1, SATURDAY – MAY 2, SUNDAY
Workshop Program
Conference Venue: Lecture Hall of Institute for Advanced Study in Mathematics,1st floor of east 7th teaching building, Zhejiang University(ZijingangCampus)
May 1, Saturday – May 2, Sunday
May 1, Saturday | |
8:30 - 9:00 AM | Registration Session |
9:00 - 10:00 AM | 李志远 Compactifications of moduli space of K3 surfaces |
10:00 - 10:15 AM | Group Photo |
10:15 – 10:30 AM | Break |
10:30-11:30 AM | 宋雷 Generic inner projection and Castelnuovo-Mumford regularity of structure sheaves |
Lunch Break |
|
2:00 - 3:00 PM | 杨成浪 Representing Kontsevich-Witten and Brezin-Gross-Witten tau-functions as Schur Q-polynomials |
3:10 - 4:10 PM | 杨迪 The Hodge-FVH Correspondence |
4:10 - 4:30 PM | Tea Break |
4:30 - 5:30 PM | 陈泽滢 Integrable stochastic dualities and the deformed Knizhnik–Zamolodchikov equation |
May 2 Sunday | |
9:00-10:00 AM | 涂君武 An invitation to categorical enumerative invariants |
10:00 - 10:20AM | Break |
10:20-11:20AM | 丁岩峭 Asymptotics of real double Hurwitz numbers |
11:30-12:30 AM | 张庆生 Polynomial structures in enumerative geometry |
Lunch Break |
|
2:30 - 3:30 PM | 周杰 Regularized integrals on Riemann surfaces and holomorphic anomaly equations |
3:40 - 4:40 PM | 李镛 Modularity via resurgence theory |
4:40 - 5:00 PM | Tea Break |
5:00 - 6:00 PM | 桂政平 Quantum master equation and chiral homology |
INVITED SPEAKERS
李志远 | 上海数学中心 |
宋雷 | 中山大学 |
杨成浪 | 北京大学 |
杨迪 | 中国科学技术大学 |
陈泽滢 | 中国科学技术大学 |
涂君武 | 上海科技大学 |
丁岩峭 | 郑州大学 |
张庆生 | 北京大学 |
周杰 | 清华大学 |
李镛 | 陈省身数学研究所 |
桂政平 | 清华大学 |
ABSTRACT
May 1
李志远 |
上海数学中心 |
Title: Compactifications of moduli space of K3 surfaces |
Abstract: In past decades, the compactifications of moduli space of K3 surfaces has received a lot of attentions from different aspects, such as birational geometry, complex geometry, arithmetic and mathematical physics. In this talk, I will survey some recent progress on in this direction, including the the KSBA compactifications, K-stable compactifications and arithmetic compactifications. I will also mention how to investigate the connections between those compactifications via the log minimal model program. |
宋雷 |
中山大学 |
Title:Generic inner projection and Castelnuovo-Mumford regularity of structure sheaves |
Abstract: Castelnuovo-Mumford regularity in a sense measures the complexity of coherent sheaves on a projective space. A. Noma established a sharp bound for the C-M regularity of structure sheaves of smooth subvarieties. A key tool is his classification of projective subvarieties via generic inner projection. I will explain Noma's classification, and show how blending it with the positivity of double-point divisors and the theory of multiplier ideals leads to the same bound for normal projective varieties with at worst isolated, $\mathbb{Q}$-Gorenstein singularities. By contrast, such a bound fails for varieties in general. This is based on a joint work with J. Moraga and J. Park. |
杨成浪 |
北京大学 |
Title:Representing Kontsevich-Witten and Brezin-Gross-Witten tau-functions as Schur Q-polynomials |
Abstract: In this talk, I will introduce our recent works on representing the Kontsevich-Witten and Brezin-Gross-Wittentau-functions as linear combinations of Schur Q-polynomials. These expressions are conjectured by Mironov -Morozov and Alexandrov respectively. The KW and BGW tau-functions are generating functions for intersection numbers on the moduli spaces of stable curves. Both of them are tau-functions of KdV hierarchy and have matrix models' descriptions in physics, which are related to the 2D topological gravity and lattice gauge theory respectively. The Schur Q-polynomials are related to the projective representations of symmetric groups, and are polynomial tau-functions of BKP hierarchy. In this talk, I will review them, and talk about our proofs of above conjectures. The talk is based on joint works with Xiaobo Liu. |
杨迪 中国科学技术大学 |
Title:The Hodge-FVH Correspondence |
Abstract: Using the Virasoro constraints we derive the loop equations for the cubic Hodge partition function with three parameters p, q, r satisfying the Calabi-Yau condition pq + qr + rp = 0. We show that the corresponding Hodge integrable hierarchy is normal Miura equivalent to the fractional Volterra hierarchy. In the procedure of the proof, a particular tau-function for the fractional Volterra hierarchy is constructed. When one of the three parameters p, q, r is equal to 1, we also prove a certain gap condition for the logarithm of the particular tau-function. The talk is based on joint works with Boris Dubrovin, Si-Qi Liu, Youjin Zhang and Chunhui Zhou. |
陈泽滢 |
中国科学技术大学 |
Title: Integrable stochastic dualities and the deformed Knizhnik–Zamolodchikov equation |
Abstract: We present a new method for obtaining duality functions in multi-species asymmetric exclusion processes (mASEP), from solutions of the deformed Knizhnik–Zamolodchikov equations. Our method reproduces, as a special case, duality functions for the self-dual single species ASEP on the integer lattice. |
May 2
涂君武 |
上海科技大学 |
Title: An invitation to categorical enumerative invariants |
Abstract: In this talk, we survey recent progresses on categorical enumerative invariants (CEI) defined by Costello back in 2005. We shall present a sketch of its definition, its explicit formula in terms of summation over graphs, as well as known computed cases. In the end, we discuss how CEI are related to GW theory, FJRW theory, and BCOV theory. |
丁岩峭 |
郑州大学 |
Title: Asymptotics of real double Hurwitz numbers |
Abstract: As the real counterpart of double Hurwitz number, real double Hurwitz number depends on the distribution of branch points. J. Rau established a lower bound for these numbers by using the tropical computation of real double Hurwitz number. We will introduce an improvement of Rau’s construction and prove the logarithmic equivalence of real and classical Hurwitz numbers. For other Hurwitz type real counting problem, a po-tential generalization of this method will also be discussed here. Part of this talk is based on a work in progress joint with Qinhao He. |
张庆生 |
北京大学 |
Title: Polynomial structures in enumerative geometry |
Abstract: It is important to calculate the enumerative invariants from various moduli theories in mirror symmetry. The generating functions of these invariants are usually expressed as formal power series in infinitely many variables which make it hard to get closed formulas. For each genus, it is conjectured that the computation of infinite many enumerative invariants can be converted to a finite computation problem, known as the polynomial structure or the finite generation conjecture. In this talk, the polynomial structure in Gromov-Witten theory and Fan-Jarvis-Ruan-Witten theory with semi-simple Frobenius structure will be proved by Virasoro constraints, and an effective method to compute generating functions will also be introduced. This talk is based on the joint work with Jian Zhou and Shuai Guo. |
周杰 |
清华大学 |
Title: Regularized integrals on Riemann surfaces and holomorphic anomaly equations |
Abstract: Integrals over configuration spaces have made their frequent appearances through Feynman graph integrals (such as in 2d chiral CFTs) and their various mathematical disguises in recent studies of Gromov-Witten theory and mirror symmetry. These integrals are constructed out of Green's functions and usually have serious divergences. My talk will be focused on explaining how to intrinsically regularized these divergent integrals for the case of Riemann surfaces without having to deal with (in particular, multiply) distributions by using the complex-analytic structure of Riemann surfaces, and discussing properties of these integrals. I will first outline the definition of our notion of regularized integrals, then some of their main properties with examples, and finally applications in mirror symmetry for elliptic curves. The talk will be based on recent joint works with Si Li. |
李镛 |
陈省身数学研究所 |
Title: Modularity via resurgence theory |
Abstract: We introduce Borel-Laplace summation in resurgence theory and use it to deal with partial theta functions, which can be written in a form of Laplace transform of a germ on Borel plane. The germ will be decomposed by odd and even parts. The odd part under Laplace transform will give us the asymptotic behavior and the even part will support a property of modularity. This is a joint work with Li Han, David Sauzin and Shanzhong Sun. |
桂政平 |
清华大学 |
Title: Quantum master equation and chiral homology |
Abstract: We study the effective BV quantization theory for chiral deformation of two dimensional conformal field theories. We explain a connection between the quantum master equation and the chiral homology for vertex operator algebras. As an application, we construct correlation functions of the curved beta-gamma system and establish a coupled equation relating to chiral homology groups of chiral differential operators. This construction can be viewed as the vertex algebra analogue of the canonical trace map in algebraic index theory and will lead to an algebraic analogue of elliptic index theory. This talk is based on a joint work with Si Li. |
GENERAL INFORMATION
REGISTRATION
Date:14:00-21:00, April 30
Venues:
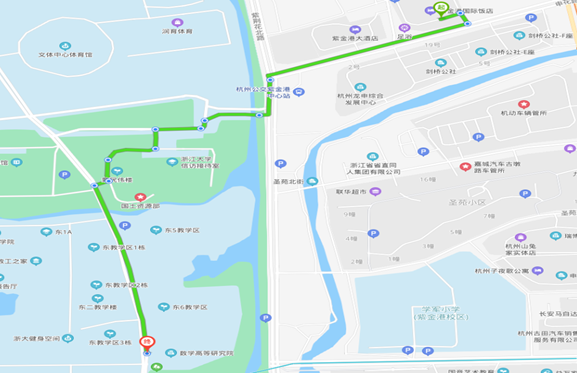
浙江紫金港国际饭店Zhejiang Zijingang International Hotel
Address: 杭州市西湖区申花路796号
No.796, Shenhua Road, West Lake District, Hangzhou.
ACCOMMODATION
Address:
浙江紫金港国际饭店Zhejiang Zijingang International Hotel
杭州市西湖区申花路796号 No.796, Shenhua Road, West Lake District, Hangzhou
BANQUET
Date:18:30-20:30, May 1, Saturday
Venue: 浙江紫金港国际饭店二楼16号厅
No.16 Dinning hall, 2nd floor, Zhejiang Zijingang International Hotel
地图MAP
ORGANIZING COMMITTEE
Yongbin Ruan Zhejiang University |
CONTACT |
|
Ran Ji E-mail: ranji02@zju.edu.cn Tel:0571-88208763 Zhejiang University China |
|




